Next we need to find the total mass of the rectangle. Lets turn to more general laminas.

Where Does The Centre Of Mass Of A Uniform Rectangular Lamina Lie Youtube
If the density at any point is the product of the distances of the point from two adjacent sides AB and AD.

. If you suspend the plate from front and back edges that will tell you whether the CM is actually in the plane in the centre of the two faces. Step-by-step solution Step 1 of 3 RESEARCH. Find the center of mass and the moment of inertia about the y-axis for a thin rectangular plate cut from the first quadrant by the lines x 6 and y 1 if 8 xy 3x y 5.
A representative rectangle of the lamina. DM ρ x btdy Now we will find the mass moment of inertia of the elemental strip about the x-axis. This balance point is often called the center of mass of the body.
That would be interesting. X 2 3 c m. Let its thickness be dy and s be the mass per unit volume of the plate.
At the other end it is 200 gcm 2. M 0 1 6 x 2 d x 3 g so the x coordinate of the center of mass is. The center of mass of this rectangle is x if x i2 x i f x i 2 as shown in the following figure.
For example the balance point of an empty see-saw is the exact center. The centroid is the term for 2-dimensional shapes. Calculate the x-coordinate of the center of mass xcm of the metal plate.
Finding the equivalent force is really the problem of finding the point where we could exactly balance the plate. 1 Since it is a point mass system we will use the equation mixiM. A 1 5 3 15cm2 Subtract the area and first moment of the circular cutout.
X x f x y d x d y Total Mass. A uniform rectangular plate of length B 38 cm and height A 25 cm has a rectangular corner cut out of it of length D 11 cm and height C 10 cmThe plate is made of a material of area mass density σFor this problem we set the origin at the lower left corner of the plate with the x-axis horizontal pointing right and the y-axis vertical pointing up. I think to find out center of mass we need to evaluate double integral.
At one end it is 500 gcm 2. Area of larger rectangle. The Symmetry Principle If a region R is symmetric about a line then the centroid of R lies on.
Find the center of mass of a rectangular plate of length 200 cm and width 100 cm. M1 3 x1 2 m2 1 x2 4 m3 5 x3 4 Solution. For laminas that are rectangular in shape we can guarantee that the center of mass or centroid is located at the center of the rectangle or where the diagonals intersect.
Problem A 20-kg rectangular metal plate is connected to a 7-kg thin cylindrical rod at its top left corner. Mass of the rectangular body density x volume M ρ x bdt Mass of the elemental section. I y 2 dM I ρ b dy ty 2.
The mass density varies linearly along the length. If your plate has cut-outs it is just possible that the CM may lie actually in one of the cutouts. The mass is M ρArea of plate ρ b a f x gx dx M ρ Area of plate ρ a b f x g x d x Next well need the moments of the region.
Based on this understanding it is clear that the center of mass of a rectangular lamina is the point where the diagonals intersect which is a result of the symmetry principle and it is stated here without proof. Homework Equations well Xcm m 1 x 1 m 2 x 2 m 1 m 2 The Attempt at a. Assuming that AB and AD are alongside of X-axis and Y-axis respectively.
Theorem 211 The Symmetry Principle. The coordinate of the center of mass of the rectangular is Here the mass of the plate is. The coordinates of their centres of mass are x3 5 and x4 9.
If the density and thickness of the plate is homogeneous the mass is proportional to the area. I want to find the center of mass of thin flat plate with constant density δ 3 g c m 2 as shown in figure. The circle has a radius of 2 and it starts at 1 to 5.
It depends on how think the plate is as to whether thats relevant. A uniform flat plate of metal with a circular hole where it is a rectangle starting from -6 to 7 from the length and the height is -3 to 3. What are the coordinates of the center of mass.
Let ρ ρ represent the density of the lamina note that ρ ρ is a constant. Now lets say we have a general lamina R where the region is bounded by two vertical lines x. The mass of the plate is.
Well first need the mass of this plate. X Type an integer or a simplified fraction y1. For a rectangle that point is both the horizontal and vertical center of the rectangle.
Find the center of mass of the system with given point masses. For symmetric objects the balance point is usually easy to find. Consider the plate as a sum of two bodies a rec- tangle of mass m3 60 units and a triangle of negative mass m1 -9 units Fig.
Based on this understanding it is clear that the center of mass of a rectangular lamina is the point where the diagonals intersect which is a result of the symmetry principle and it is stated here without proof. The rod is connected to the roof by a frictionless pin joint that is free to swing. 2 Lets multiply each point mass and its displacement then sum up those products.
There are two moments denoted by M x M x and M y M y. 15m 1C₂ C1 is the center of mass of the plate alone and C2 is the center of mass of the rod. Namely finding the equations of the boundary lines of a plate.
M y 0 1 6 x 2 d x 2 g. The coordi- nate of the centre of mass is xcm1x1m2x2m1m29xx142xx55143 Second method. A sheet of this paper that is 1 m by 1 m will have a mass of 80 g.
This video demonstrates a first step in finding the centre of mass of a plate. So we want to find the center of mass of the region below. The moment of the plate about y a x i s is therefore.

Find The Moment Of Inertia Of A Uniform Rectangular Plate Of Mass M And Edges Of Length I Youtube
Mechanics Map 3d Centroid And Mass Moment Of Intertia Table

Solved Derive The Expression For The Moment Of Inertia About Chegg Com
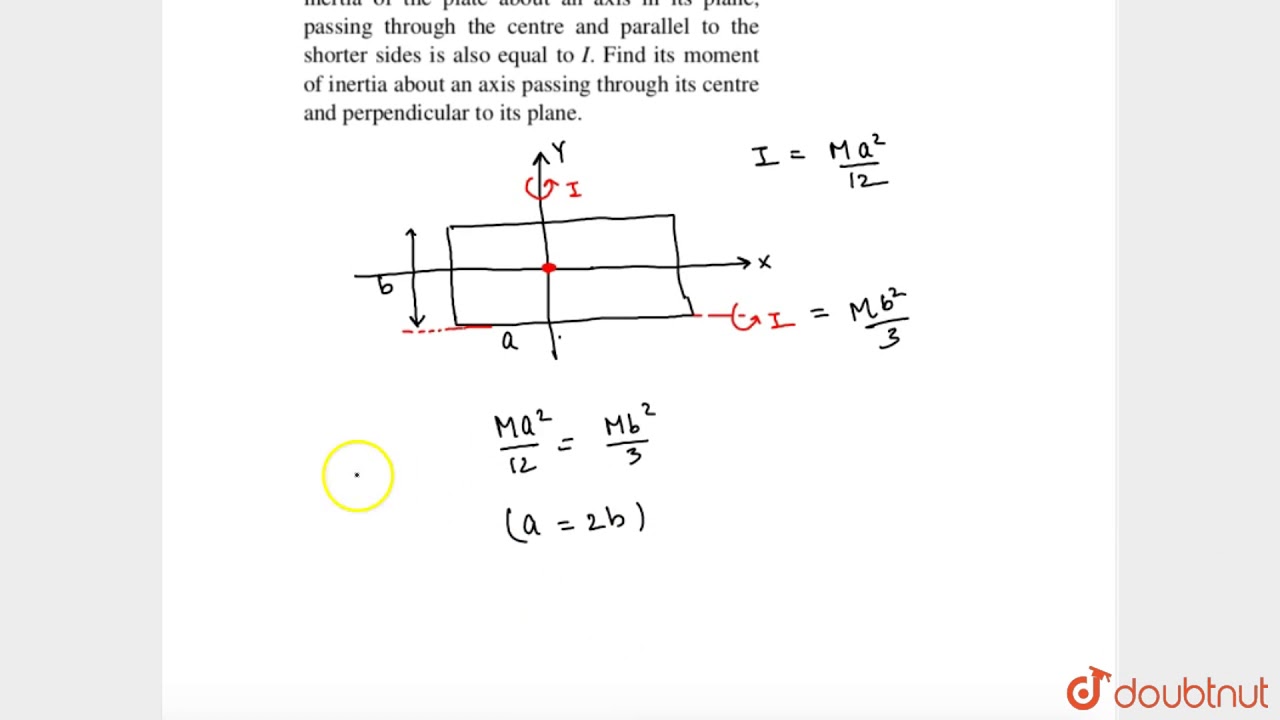
A Uniform Rectangular Plate Has Moment Of Inertia About Its Longer Side Equal To I The Youtube
0 Comments